Delving into the realm of geometry, we present the Surface Area Triangular Prism Worksheet, an invaluable tool for students seeking to enhance their understanding of this fundamental concept. This comprehensive worksheet equips learners with the knowledge and skills necessary to calculate the surface area of triangular prisms, empowering them to solve complex problems with confidence.
As we embark on this mathematical journey, we will explore the intricacies of triangular prisms, unraveling their unique characteristics and the impact they have on surface area calculations. Through a step-by-step approach, we will guide you through the process of determining base area and lateral surface area, providing ample practice problems to reinforce your understanding.
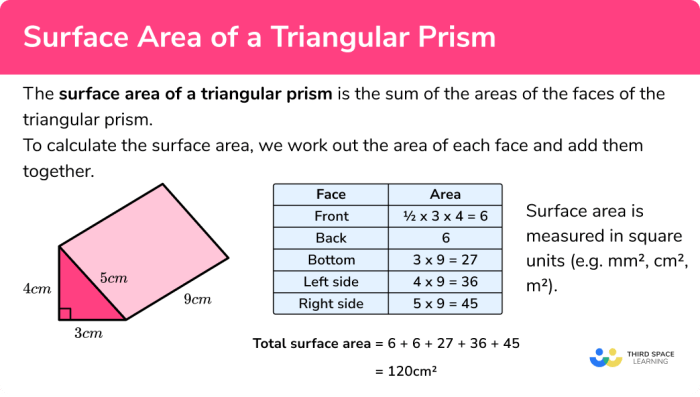
Surface Area of a Triangular Prism
The surface area of a triangular prism is the total area of all its faces. It is calculated by summing the areas of the two triangular bases and the three rectangular lateral faces.
The formula for calculating the surface area (SA) of a triangular prism is:
SA = 2(1/2
- b
- h) + 3
- l
- w
where:
- b is the base length
- h is the height of the triangle base
- l is the length of the lateral faces
- w is the width of the lateral faces
Determining Base Area and Lateral Surface Area
The base area of a triangular prism is the area of one of its triangular faces. It is calculated using the formula for the area of a triangle: (1/2) – b – h.
The lateral surface area of a triangular prism is the sum of the areas of its three rectangular lateral faces. It is calculated by multiplying the length (l) of a lateral face by its width (w) and then multiplying the result by 3.
Types of Triangular Prisms
Triangular prisms can be classified into two main types: regular and irregular.
Regular Triangular Prisms, Surface area triangular prism worksheet
- Have a triangular base with all three sides equal in length.
- Have three rectangular lateral faces that are congruent.
- Have equal base angles and equal lateral face angles.
Irregular Triangular Prisms
- Have a triangular base with sides of unequal lengths.
- May have rectangular lateral faces that are not congruent.
- May have unequal base angles and unequal lateral face angles.
The type of prism affects the calculation of its surface area. For regular triangular prisms, the base area and lateral surface area can be calculated using the formulas provided above. For irregular triangular prisms, the base area and lateral surface area must be calculated separately using the appropriate formulas.
Calculating Surface Area: Step-by-Step
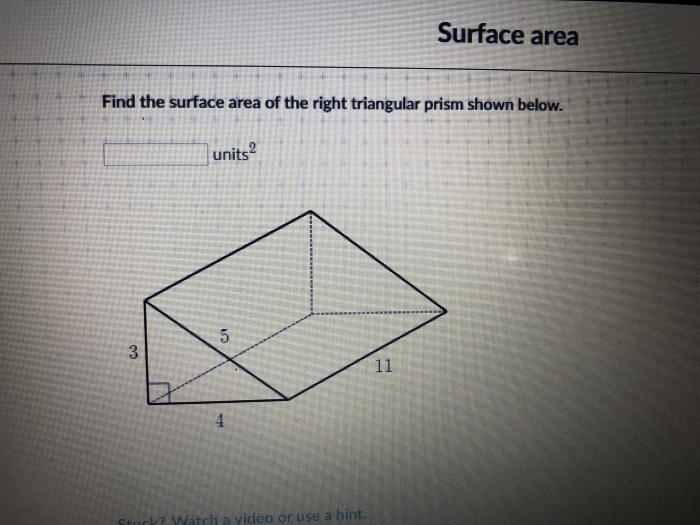
To calculate the surface area of a triangular prism, follow these steps:
- Calculate the base area using the formula: (1/2)
- b
- h.
- Calculate the lateral surface area using the formula: 3
- l
- w.
- Add the base area and lateral surface area to get the total surface area.
Example:
Calculate the surface area of a triangular prism with a base length of 5 cm, a base height of 3 cm, a lateral face length of 4 cm, and a lateral face width of 2 cm.
Step 1:Calculate the base area: (1/2) – 5 cm – 3 cm = 7.5 cm 2
Step 2:Calculate the lateral surface area: 3 – 4 cm – 2 cm = 24 cm 2
Step 3:Calculate the total surface area: 7.5 cm 2+ 24 cm 2= 31.5 cm 2
Real-World Applications
Surface area calculations have numerous practical applications in everyday life, including:
- Packaging:Calculating the surface area of a package helps determine the amount of material needed and the cost of packaging.
- Construction:Calculating the surface area of a building helps determine the amount of materials needed for construction and the cost of materials.
- Design:Calculating the surface area of an object helps determine its shape, appearance, and functionality.
For example, in the construction industry, surface area calculations are used to determine the amount of paint needed to cover a building’s exterior or the amount of siding needed to cover a house.
Practice Problems: Surface Area Triangular Prism Worksheet
- Calculate the surface area of a triangular prism with a base length of 4 cm, a base height of 3 cm, a lateral face length of 5 cm, and a lateral face width of 2 cm.
- A regular triangular prism has a base side length of 6 cm and a height of 5 cm. Calculate its surface area.
- An irregular triangular prism has a base area of 12 cm2and a lateral surface area of 30 cm 2. Calculate the total surface area of the prism.
Solutions:
- 34 cm2
- 90 cm 2
- 42 cm 2
Clarifying Questions
What is the formula for calculating the surface area of a triangular prism?
Surface Area = 2 – Base Area + Lateral Surface Area
How do I determine the base area of a triangular prism?
Base Area = (1/2) – Base Length – Height
What is the difference between a regular and irregular triangular prism?
A regular triangular prism has congruent bases and lateral faces, while an irregular triangular prism has non-congruent bases and/or lateral faces.