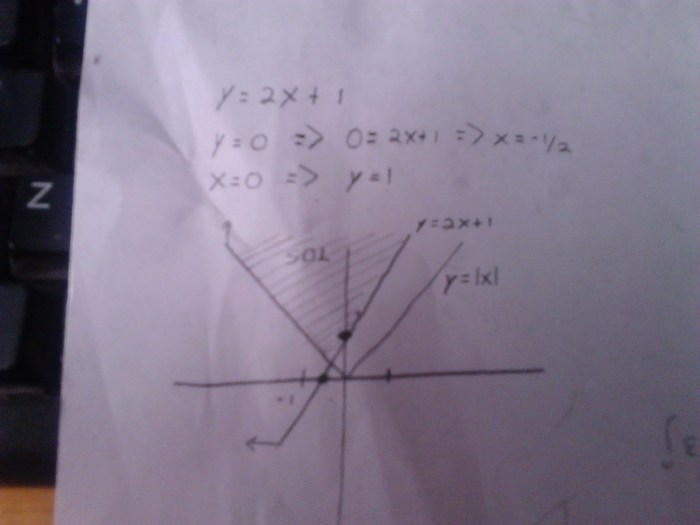
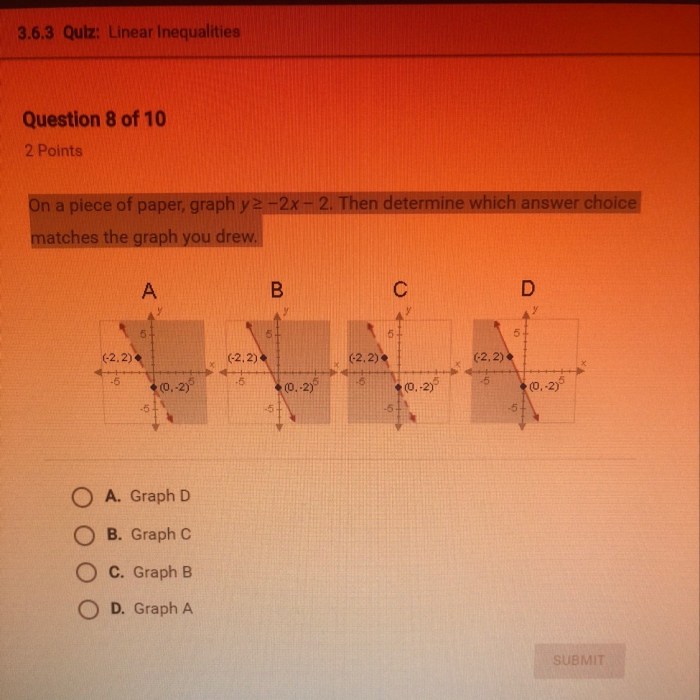
Which is the graph of linear inequality x 2y 12 – Welcome to the realm of linear inequalities! Embark on a journey to unravel the mysteries of x ≥ 2y + 12, where we’ll delve into the art of graphing linear inequalities, exploring their real-world applications and gaining a deeper understanding of their significance.
In this comprehensive guide, we’ll navigate through the intricacies of graphing linear inequalities, starting with the fundamentals and progressing to advanced concepts. Along the way, we’ll uncover the secrets of plotting boundary lines, shading solution regions, and testing points to determine their validity.
Graphing Linear Inequality
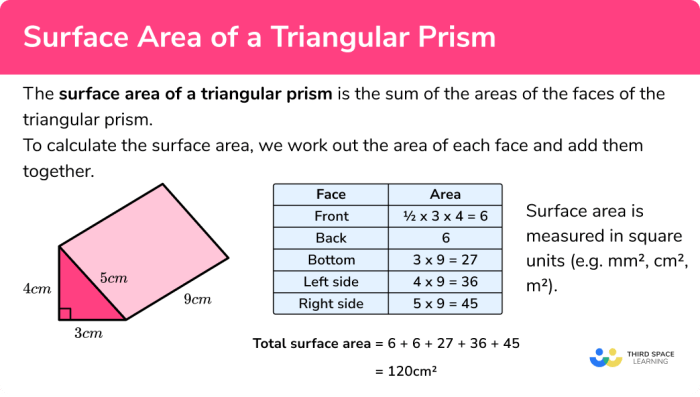
Linear inequalities are mathematical statements that compare two linear expressions. They can be represented graphically as regions on a coordinate plane. The graph of a linear inequality consists of a boundary line and a shaded solution region.
Plotting the Boundary Line
The boundary line is the line that represents the linear equation obtained by replacing the inequality symbol with an equality symbol. To plot the boundary line, determine the slope and y-intercept of the line using the slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept.
Plot the line using these values, ensuring a dashed line for inequalities with < or > symbols and a solid line for inequalities with ≤ or ≥ symbols.
Shading the Solution Region
The solution region is the area of the coordinate plane that satisfies the inequality. To shade the solution region, determine whether the inequality symbol is ≥ or ≤. Shade the region above the boundary line for ≥ and below the boundary line for ≤.
Testing Points, Which is the graph of linear inequality x 2y 12
To verify if a point lies within the solution region, substitute its coordinates into the inequality. If the inequality holds true, the point lies within the solution region. Testing multiple points helps ensure the accuracy of the shaded region.
Real-World Applications
Linear inequalities have numerous real-world applications. For example, the inequality x ≥ 2y + 12 can be used to determine the feasible production quantities of two products with different profit margins.
Question Bank: Which Is The Graph Of Linear Inequality X 2y 12
What is a linear inequality?
A linear inequality is a mathematical statement that compares two linear expressions using an inequality symbol, such as x ≥ 2y + 12.
How do I graph a linear inequality?
To graph a linear inequality, first plot the boundary line and determine whether it should be dashed or solid. Then, shade the solution region, which is the area that satisfies the inequality.
What are some real-world applications of linear inequalities?
Linear inequalities have numerous real-world applications, such as optimizing resources, determining feasibility constraints, and modeling growth and decay.