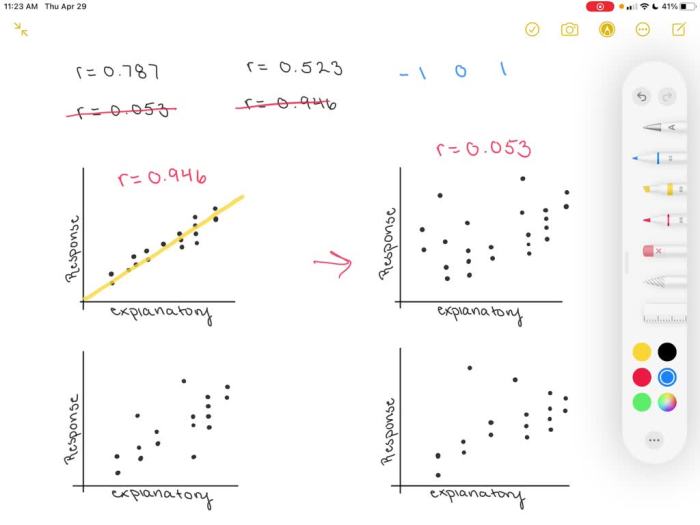
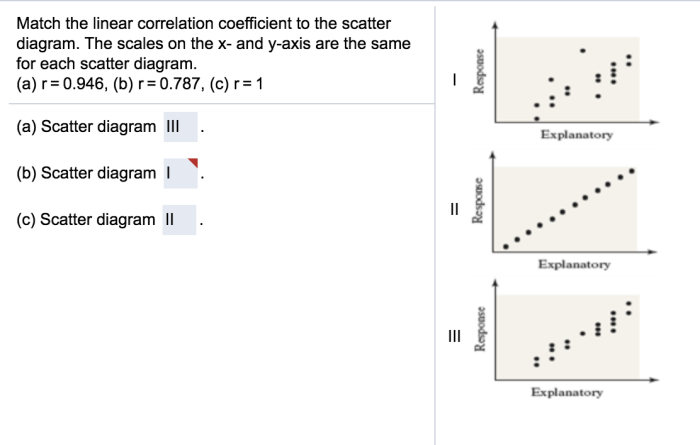
Match the linear correlation coefficient to the scatter diagram – As we delve into the realm of statistics, the interplay between the linear correlation coefficient and the scatter diagram emerges as a crucial concept. This article embarks on an exploration of their intricate relationship, unraveling the secrets behind their ability to reveal patterns and quantify the strength of linear associations.
The scatter diagram, a visual representation of data points, provides a graphical depiction of the relationship between two variables. By examining the pattern of points, we can discern the strength and direction of the linear association. The linear correlation coefficient, a numerical measure, quantifies this relationship, ranging from -1 to 1, indicating the degree and direction of the linear trend.
Correlation Coefficient and Scatter Diagram Relationship
The linear correlation coefficient (r) is a statistical measure that quantifies the strength and direction of the linear relationship between two variables. It ranges from -1 to 1, where:
- r = 1 indicates a perfect positive linear relationship, where the points in the scatter diagram form a straight line that slopes upward.
- r = 0 indicates no linear relationship, where the points in the scatter diagram are randomly scattered.
- r = -1 indicates a perfect negative linear relationship, where the points in the scatter diagram form a straight line that slopes downward.
Scatter Diagram Interpretation
A scatter diagram is a graphical representation of the relationship between two variables. Each point in the scatter diagram represents a pair of data values. The pattern of points in a scatter diagram can provide visual cues about the strength and direction of the linear relationship between the variables.
For example, a scatter diagram with points that form a straight line indicates a strong linear relationship. The slope of the line indicates the direction of the relationship (positive or negative). A scatter diagram with points that are randomly scattered indicates no linear relationship.
Matching Correlation Coefficient to Scatter Diagram
The following table provides a visual representation of how the correlation coefficient relates to the pattern of points in a scatter diagram:
| Correlation Coefficient | Scatter Diagram Pattern |
|---|---|
| 1 | Straight line with a positive slope |
| 0 | Randomly scattered points |
| -1 | Straight line with a negative slope |
Real-World Applications, Match the linear correlation coefficient to the scatter diagram
Matching the correlation coefficient to the scatter diagram is a useful technique in various fields, including:
- Data analysis:Identifying trends and relationships in data.
- Predictive modeling:Developing models to predict future outcomes based on historical data.
- Hypothesis testing:Testing hypotheses about the relationship between variables.
Limitations and Considerations
While correlation is a useful tool for quantifying the strength and direction of a linear relationship, it is important to note that correlation does not imply causation. There may be other factors that are influencing the relationship between the variables.
Additionally, the interpretation of a scatter diagram can be affected by outliers, which are data points that are significantly different from the rest of the data. Outliers can distort the pattern of points and make it difficult to determine the true relationship between the variables.
User Queries: Match The Linear Correlation Coefficient To The Scatter Diagram
What is the linear correlation coefficient?
The linear correlation coefficient is a numerical measure that quantifies the strength and direction of a linear relationship between two variables. It ranges from -1 to 1, with -1 indicating a perfect negative correlation, 0 indicating no correlation, and 1 indicating a perfect positive correlation.
How is the linear correlation coefficient related to the scatter diagram?
The linear correlation coefficient is calculated based on the pattern of points in a scatter diagram. A positive correlation coefficient corresponds to a positive slope in the scatter diagram, while a negative correlation coefficient corresponds to a negative slope. The strength of the correlation is reflected in the tightness of the points around the regression line.
What are the limitations of using correlation to determine causation?
Correlation does not imply causation. Just because two variables are correlated does not mean that one causes the other. Other factors may be influencing the relationship between the variables.